
電子技術科(都留キャンパス)No.495
令和7年9月5日(金)
高校生のみなさん、こんにちは!
今回は、2年生の『線形代数学Ⅱ』の授業をご紹介します。
前回の授業では、2×2行列の対角化に取り組みましたが、今回はレベルアップして、3×3行列の対角化に挑戦しました!
行列は、コンピュータがビッグデータやAIの学習データを扱うときに欠かせない、重要な数学的ツールです。そのため、最近の高校数学では「数学C」が復活し、2×2行列の演算や変換など、基本的な内容が学べるようになりました。
今回の記事では、さらに一歩進んで「3×3行列の対角化」に挑戦します!これは大学以降で扱う内容ですが、ちょっと先取りして楽しんでいただけたら嬉しいです!
➀ まずは問題にチャレンジ!
今回の演習では、3×3の行列Aを対角化することが目標です。
対角化には、3本の固有ベクトルが必要になります。
(※固有ベクトルが3本そろえば、行列Aは対角化可能です)

② 固有値を求めよう!
まずは、行列Aから「λ倍の単位行列」を引いたものを使って、固有値を求める式を立てます。
この式を解くことで、行列Aの固有値が見つかります。

③ 固有値は「重解」と「単解」
今回の行列では、式を因数分解すると、
同じ値が2回出てくる「重解」と、
1回だけ出てくる「単解」の固有値が見つかりました。
今回は、「1」という固有値が2回出てきて、「3」が1回だけ出てきました。

💡補足:重解ってなに?
「重解(じゅうかい)」とは、同じ答えが何回も出てくることです。
今回のように、「1」という答えが2回出てきたら、それは「重解」です。
また、固有値が「2回同じだった」場合、それを「重解の固有値」と呼びます。
そして、その固有値に対して何本の固有ベクトルが見つかるかがとても大事です。
今回の演習では、重解の固有値に対して2本の固有ベクトルが見つかったので、
行列を対角化することができました!
④ ランクを調べて効率アップ!
固有ベクトルを求めるには、連立方程式を解く必要があります。
その際、係数行列のランクを調べると、効率よく解けることがあります。
ランクとは、連立方程式の中で、互いに独立な(重複していない)方程式の数を表します。

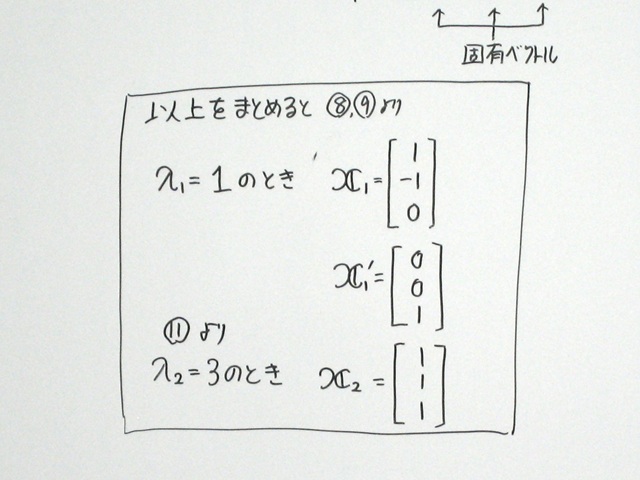
⑤ 固有ベクトルを求めよう!
それぞれの固有値に対応する固有ベクトルを求めます。
・ 重解の固有値 → 固有ベクトルが2本
・ 単解の固有値 → 固有ベクトルが1本
これで、3本の固有ベクトルがそろいました!
⑥ 変換行列Pを作成!
3本の固有ベクトルを並べて、変換行列Pを作ります。
この行列Pを使って、元の行列Aを対角化していきます。

⑦ 逆行列P⁻¹を求めよう!
変換行列Pの逆行列P⁻¹を、掃き出し法を使って求めます。
掃き出し法は、行列の計算を効率よく進めるための便利な手法です。

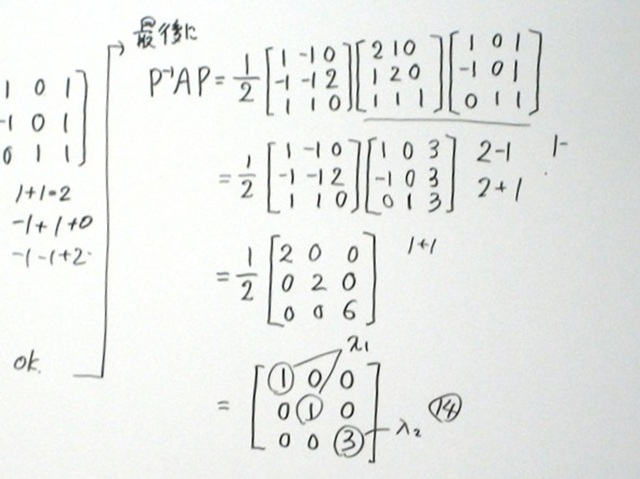
⑧ いよいよ対角化!
最後に、変換行列Pとその逆行列を使って、行列Aを対角化します。
対角化された行列では、対角の部分に固有値がきれいに並びました!
🎓まとめ
3×3行列の対角化も、無事に成功しました!
演習では3×3までの行列を扱いますが、AIやニューラルネットワークの世界では、もっともっと大きな行列が登場します。
次回の授業紹介もお楽しみに!
それではまた!