
電子技術科(都留キャンパス) No.496
📅令和7年9月8日(月)
高校生のみなさん、こんにちは!
今日は、2年生が演習問題『スマホの使用時間と睡眠時間の関係』に取り組みました。
この課題は、単回帰分析を用いたデータ解析の演習であり、ニューラルネットワークの考え方にもつながる、非常に重要な基礎的内容です。
➀ 単回帰分析の課題とは?
中学生3名の「スマホの使用時間」と「睡眠時間」のデータをもとに、スマホの使用時間から睡眠時間を予測するモデルを構築します。
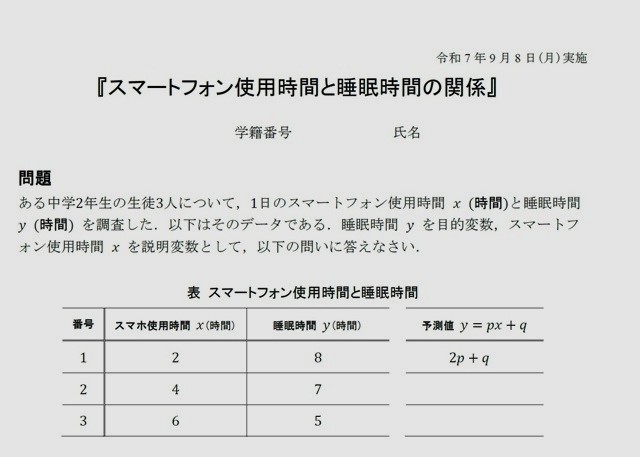
② 計算モデルの決定
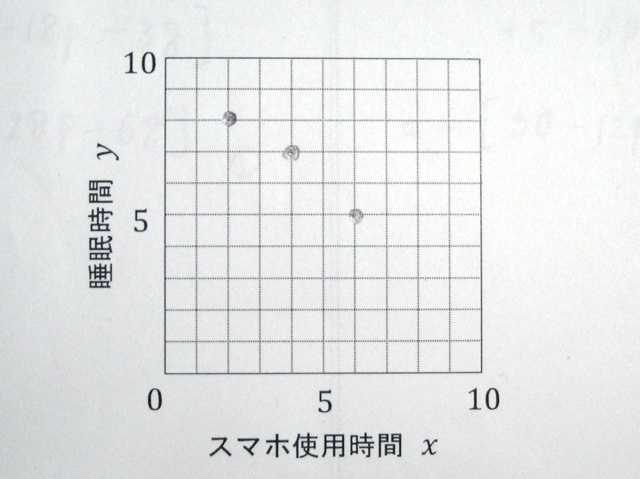
まずは、3名分のデータを散布図にプロットし、傾向を確認します。
散布図から、睡眠時間はスマホの使用時間に対して「直線的」に変化しているようです。
したがって、モデルは「一次関数(直線)」で表せそうですね。
③ モデルのパラメータ設定
直線モデル y=px+q のパラメータは「傾き p」と「切片 q」です。
このモデルを使って、スマホの使用時間から睡眠時間を予測します。

④ 2乗誤差の総和を計算
モデルによる予測値と実際のデータとの差を2乗し、その総和を求めます。
これが「2乗誤差の総和(損失関数)」です。

⑤ 偏微分の計算
後の最適化に備えて、2乗誤差の総和をパラメータ p, q で偏微分します。

⑥ 最適化条件からパラメータを求める(解析的アプローチ)
偏微分の結果がゼロとなる条件から、p と q を求める連立方程式を導出します。
この連立方程式を行列を使って手計算で解き、最適な p, q の値を求めました。

⑦ 勾配降下法による最適化(数値的アプローチ)
次に、勾配降下法を用いて、パラメータ p と q の値を少しずつ変化させながら、
2乗誤差の総和が最小となる値を探索するアルゴリズムを PAD で設計しました。
この方法は「数値的アプローチ」と呼ばれ、パソコンを使って繰り返し計算を行うことで、最適なパラメータに近づいていきます。

⑧ 2つの手法の比較(解析的 vs 数値的)
連立方程式を解く方法は「解析的アプローチ」であり、数学的な式を使って手計算で一度に p と q の値を求める方法です。
一方、勾配降下法は「数値的アプローチ」であり、パソコンを使って繰り返し計算を行い、少しずつ最適解に近づいていく方法です。
今回は、両方の手法を体験することで、それぞれの特徴や使いどころの違いを学びました。

🧑🏫 先生からのひとこと
今回の授業では、数学の理論(解析的手法)と、パソコンを使った数値計算(数値的手法)の両方を体験しました。
これからの時代、数学を「使える力」として身につけることがますます重要になります。
📢それでは、次回の授業紹介もお楽しみに