
(都留キャンパス電子技術科No.475)
こんにちは。今回は、令和6年7月11日(木)1限に行われた電子技術科(都留キャンパス)1年生の講義『デジタル回路』を紹介します。産業技術短大では、基本的に講義は1時限で100分ですが、実験や実習などは2時限続きで200分になります。 入学したころにはとても長く感じた1年生も、だいぶ慣れてきたようです。
『デジタル回路』の講義では、『コンピュータ』や『デジタル機器』の動作を考える上で基本となる『論理演算』や『論理回路』について学んでいます。4月から講義がスタートして、これまでに『2進数の演算』、『論理演算』、『基本論理素子』、『組み合わせ論理回路』、『フリップフロップ回路』について学んできました。
いよいよ今回からは、これまでに学んだ回路を応用した『カウンタ回路』について学んでいきます。しかし、その前に前回の試験の答案用紙を返却しました。特に正答率が低かった問題については、復習をかねて解答を解説しました。

ここからが本題のスタートです。
『カウンタ回路』は、複数個の『フリップフロップ』の接続からなります。はじめに、もっとも構造がシンプルな非同期式の『アップカウンタ』から学んでいきます。

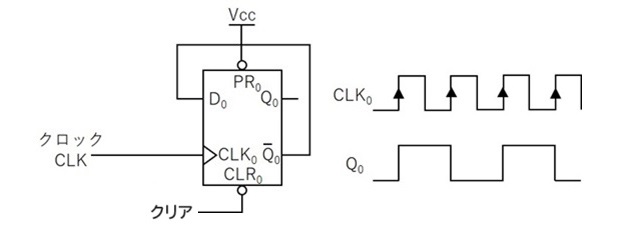
下の回路は、Dフリップフロップ1個で構成された1ビットの『カウンタ』です。まず、クリア信号を使って出力Q0の値を「0」にリセットします。このとき、反転出力notQ0の値「1」がD0に入力され、この値がクロック信号の立ち上がりに同期して出力Q0にロードされます。これにより、出力Q0の値が「0」から「1」に切り替わります。
次に、反転出力notQ0の値「0」がD0に入力され、この値がクロック信号の立ち上がりに同期して出力Q0にロードされます。これにより、出力Q0の値が「1」から「0」に切り替わります。この過程を繰り返すことで、出力Q0の値が「0」と「1」を交互に繰り返します。
この動作から、この回路が桁上がりのない『2進数カウンタ』として機能していることがわかります。
『Dフリップフロップ』の個数を増やし、これらをうまく接続することで、2ビット以上の『カウンタ』を構成することができます。例えば、『Dフリップフロップ』を2個接続して2ビットにすると、00、01、10、11のように、10進数で0から3までカウントする『4進カウンタ』ができます。また、Dフリップフロップを3個接続して3ビットにすると、000、001、・・・、111のように、10進数で0から7までカウントする『8進カウンタ』ができます。一般に『Dフリップフロップ』をn個接続してnビットにすると、10進数で0から2n-1までカウントする『2n進カウンタ』を構成することができます。

ひととおり『カウンタ』について学んだあと、演習問題に取り組みました。

演習問題では『Dフリップフロップ』を3個使用して3ビットの『カウンタ回路』を設計しました。各『フリップフロップ』の出力をタイムチャートで表すと、出力(Q2, Q1, Q0)の値が(0, 0, 0)から(1, 1, 1)までの8パターンあることが確認できました。これにより『Dフリップフロップ』を3個接続することで、『8進カウンタ』が構成できることがわかりました。
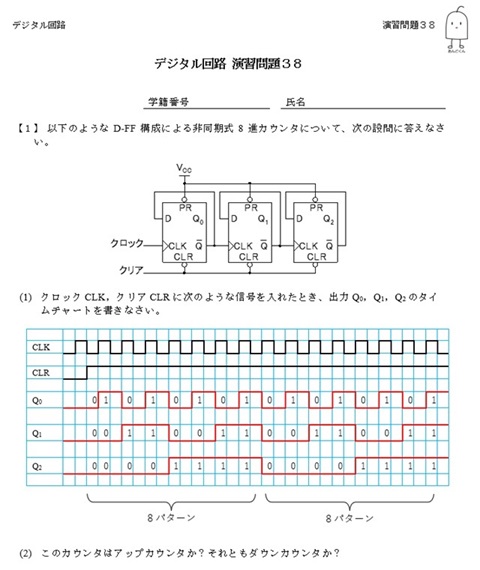
タイムチャートから、各『フリップフロップ』の出力信号(Q2, Q1, Q0)を時系列に真理値表にまとめました。(0, 0, 0)から(1, 1, 1)まで『カウントアップ』していることがわかります。この回路が『8進アップカウンタ』であることが確認できました。
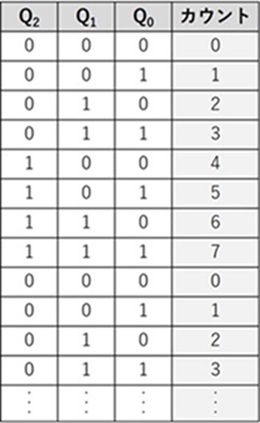
また、3個の『Dフリップフロップ』から、3ビットの『ダウンカウンタ回路』を構成することも可能です。この点については、このあとの演習問題で取り組みました。

今回はここまで。
みんな、今日も1日おつかれさま☆彡
「次回は、カウンタ回路をJKフリップフロップで構成していきます。」
今日も『産業技術短大のTopics』をみてくれてありがとう!
また、明日からがんばろっ٩( ‘ω’ )و

それじゃ≡3 ≡3 ≡3
(都留キャンパス電子技術科No.475)