
(都留キャンパス)No.507
📅 令和8年1月16日(金)
📍 電子技術科(都留キャンパス)1年生『微分方程式』の授業より
🎓こんにちは!【授業☆しょ~かい】の時間です。
このシリーズでは、電子技術科の授業を、高校生のみなさんにも分かりやすく紹介しています。
授業の雰囲気や「どんなことを学ぶの?」が、写真と一緒にイメージできる内容になっています。
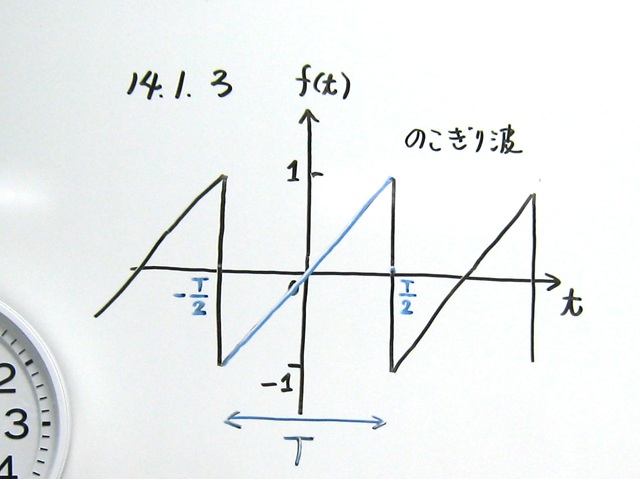
🧠 今回のテーマ:のこぎり波を分解してみよう!
電子技術科では、電子回路を理解するために
「フーリエ級数」や「フーリエ変換」といった数学を学びます。
今日はその中でも、のこぎり波という波形を“分解”してみる授業でした。
🧠 フーリエ級数って何?
フーリエ級数は、
「複雑な波を、いくつもの単純な波(sinやcos)に分けて考える方法」です。
たとえるなら…
🎵 いろんな楽器が混ざった音を、
「これはドラムの音」「これはギターの音」
と分けて聞くようなイメージ。
電子回路でも、波の中にどんな“成分”が入っているかを知ることが大事なんです。
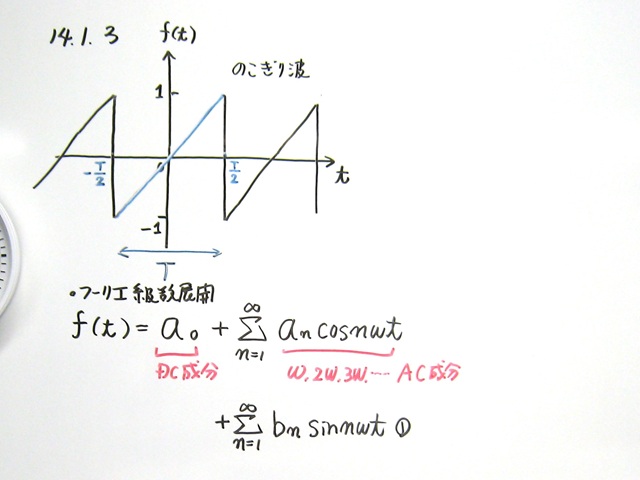
✏️ Step 1:まずは直流成分をチェック!
波の平均値(=直流成分)を調べます。
のこぎり波の性質から、直流成分はゼロになります。

✏️ Step 2:つぎは交流成分!
ここからが本番。
波を作っている“振動する成分”の大きさを計算していきます。

✏️ Step 3:交流成分は2種類ある!
交流成分には
・cosで振動する成分
・sinで振動する成分
の2つがあります。
のこぎり波の場合、cosの成分はゼロになります。
(波の形の“対称性”が理由です)
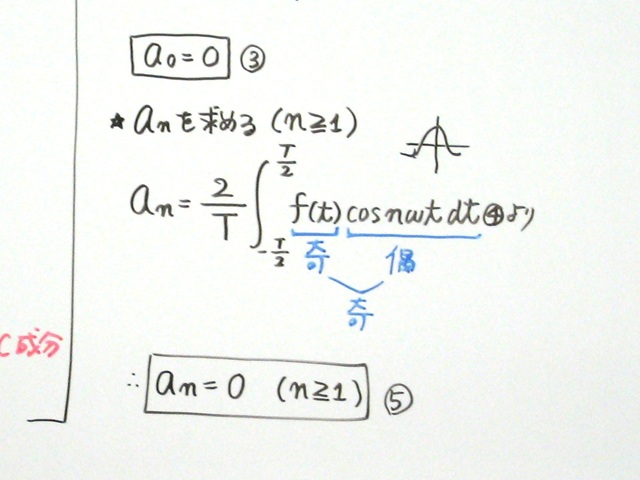
✏️ Step 4:sin成分の大きさを求める!
残った sin(nωt) の成分について、
「どれくらいの大きさなのか?」を計算します。
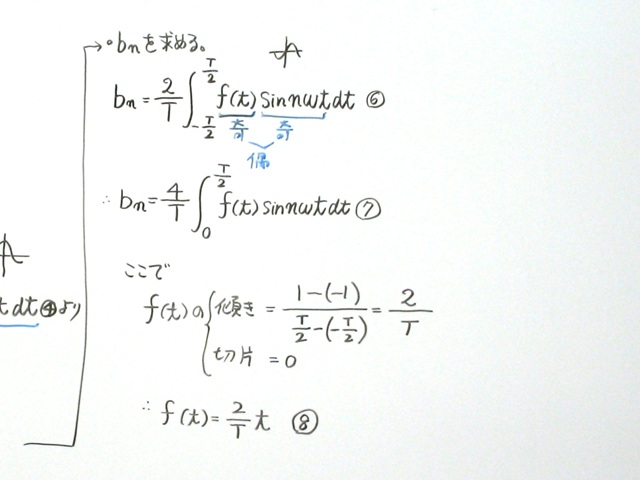
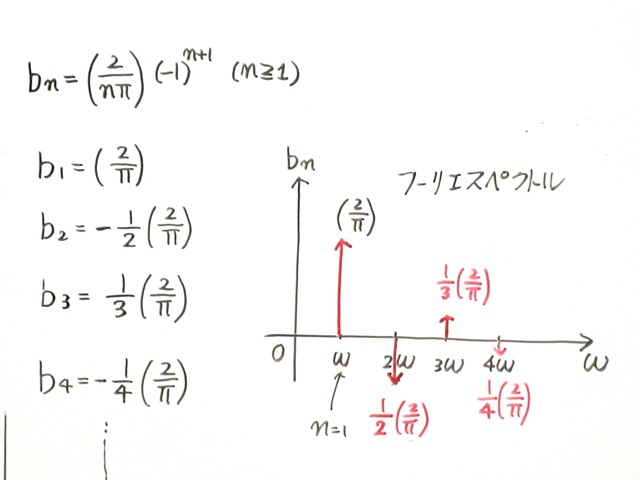
計算の結果、sin成分の係数が求まりました。

✏️ Step 5:フーリエスペクトルを描いてみた!
求めた係数をグラフにすると、
どの周波数の成分が強いのかがひと目で分かります。
これをフーリエスペクトルといいます。
🔜 次回の授業は…
次回は、周期ではない波(非周期関数)をフーリエ変換で調べる内容に進みます!
💡しょ~かいポイント!
フーリエスペクトルを見ると、
波の中にどんな“音色(周波数成分)”が入っているかが分かります。
電子回路を学ぶうえで、とても大切な考え方です。
次回の【授業☆しょ~かい】もお楽しみに!